Fitting a Polygon About a Set of Points
QUESTION: I have a set of points and I would like to calculate a polygon that completely surrounds the points. How can I do that?
![]()
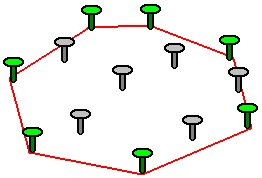
ANSWER: What you want is called the "convex hull". Imagine that your points are nails sticking into a board. If you stretched a rubberband completely around your points, so that all the points were inside the perimeter of the rubberband, the nails that the rubberband touches are the points of a polygon that is called the convex hull. See the figure below.
The convex hull can be calulated with the TRIANGULATE command. Here is an example program that illustrates the technique. It requires the FSC_Color program from the Coyote Library to run.
PRO ConvexHull
x=[0.36,0.35,0.39,0.42,0.60,0.41,0.48,0.73,0.46,0.42,0.42,0.42, $
0.47,0.44,0.47,0.49,0.54,0.64,0.65]
y=[0.19,0.26,0.26,0.26,0.14,0.22,0.15,0.10,0.16,0.30,0.27,0.27, $
0.23,0.23,0.22,0.16,0.16,0.08,0.08]
Window, XSize=350, YSize=350, Title='Convex Hull'
Plot, x, y, color=FSC_Color("Green"), /NoData, YRange=[0.0, 0.5], $
Background=FSC_Color("Charcoal", !P.Background)
Triangulate, x, y, triangles, hull
Plots, [x[hull],x[hull[0]]], [y[hull],y[hull[0]]], Color=FSC_Color("Yellow")
Plots, x, y, psym=4, Color=FSC_Color("Cyan"), Symsize=2
END
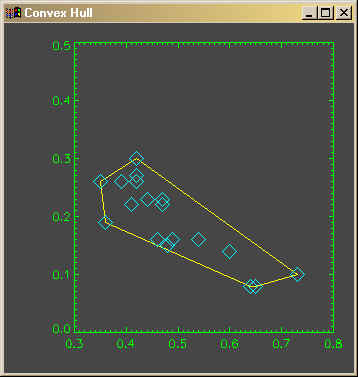
The results of the program are shown in the figure below.
![]()
Copyright © 2006 David W. Fanning
Last Updated 11 January 2006