Random Spherical Distribution of Points

QUESTION: I would like to have a random distribution of points on the surface of a sphere, but I'm having trouble with it. For some reason, when I look at the distribution I see clumping. Is this a limiation of IDL's random number generator, or am I doing something wrong? My code looks like this:

   sphericalCoords = FltArr(3, 1000)

   sphericalCoords[0,*] = RANDOMU(seed, 1000, /Uniform, /Double) * 360.0        ; Rho
   sphericalCoords[1,*] = RANDOMU(seed, 1000, /Uniform, /Double) * 180.0 - 90.0 ; Omega
   sphericalCoords[2,*] = REPLICATE(1.0D, 1000)                                 ; Radius

   Window, XSize=250, YSize=250, Title='Random Points are Clumping'
   Map_Set, 90, 0, -90, /Lambert, /Isotropic
   PlotS, sphericalCoords[0,*], sphericalCoords[1,*], PSym = 3

Notice the clumping in the center of the plot in the figure below.

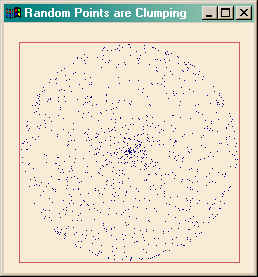
ANSWER: The answer was provided by Ken Bowman on the IDL newsgroup.

The problem is not with the IDL random number generator. The problem is with the way you are calculating your omega values. It might be easier to understand the solution if we think of the rho values as longitude angles and the omega values as latitude angles.

By selecting both randomly, we expect an equal distribution of values (approximately) in each delta omega-delta rho section. In other words, a random distribution in space. But, of course, on a sphere, these sections become progressively smaller in area as you approach the poles. That is why you see some clumping in the center (or polar) region of the figure above.

What you really want for your latitude angles is not a random distribution in space, but rather a random distribution in angle. You can obtain this by creating a random distribution of numbers between -1 and 1 ( or -90 and 90 degrees), and then calculating the angle of each of these numbers. In other words, you want the arcsine of each of these random numbers. This will be a random distribution of angles.

For example, if you calculate your omega angles like this:

   sphericalCoords[1,*] = !RADEG * ASIN(RANDOMU(seed, 1000, /Uniform, /Double) * 2.0D - 1.0D)

you will see the clumping in your random numbers disappear. See the figure below.